Gitterfüllende Kurven sind kein neues Forschungsgebiet, sie wurden bereits 1890 entdeckt. Bekannte Beispiele sind die Hilbert- und die Peano Kurve [3,4].

Eine gitterfüllende Kurve füllt einen Teil des darunterliegenden Gitters vollständig aus. Bis 2013 waren allerdings nur ein paar der Monsterkurven veröffentlicht worden. Dann begann Jörg Arndt seine Suche nach Kurven einer ganz bestimmten Klasse – und war erfolgreich! Bis heute fand er über eine Million neuer fraktaler Objekte.

Das Bild zeigt die Ersetzung des ersten „F“ - ein einfacher Strich - durch das Wort „F+F-F“. Die daraus entstehende Form, die ein wenig wie ein schiefes N aussieht, ist die erste Iteration des L-Systems. Für die nächste Iteration wird wieder jedes „F“ durch „F+F-F“ ersetzt, „+“ und „-“ bleiben unverändert.

Das Rendern der Kurven wird durch Turtle-Graphics umgesetzt. Stellt euch vor, ihr habt eine sehr geduldige Schildkröte, die für euch Linien zeichnet. Ihr setzt euch auf ihren Rücken und müsst ihr nur sagen, wie gezeichnet werden soll. Der Buchstabe „F“ bedeutet „male eine Linie in Einheitslänge in die aktuelle Richtung“. Da das unterliegende Gitter aus Dreiecken besteht, werden „+“ und „-“ als Drehungen um plus, oder minus 120° interpretiert. Auf anderen Gittern sind Drehungen um 90°, 60° und 120° möglich. Die resultierende Kurve in unserem Beispiel ist der altbekannte Terdragon, entdeckt von Davis und Knuth im Jahre 1970 [5].

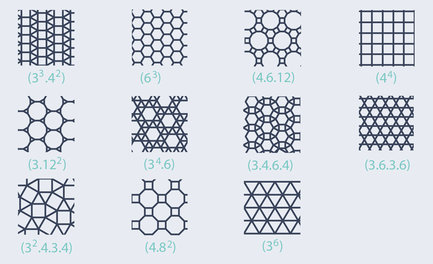
Wie bereits oben erwähnt, leben die Kurven auf bestimmten Gittern. Bei der Hilbert- oder der Peano-Kurve sieht man bereits, dass sie über ein quadratisches Gitter laufen. Die Gitterfüllenden Kurven unserer Klasse können nur auf Gittern existieren, die an jedem Punkt eine gerade Anzahl von sich treffenden Linien aufweisen. Dies ist beispielsweise beim Dreieckgitter, dem Viereckgitter und dem trihexagonalen Gitter (aus Dreiecken und Sechsecken) der Fall. Ein Gitter, das ausschließlich aus Sechsecken besteht, erfüllt diese Bedingung nicht, da sich hier drei Kanten an jedem Punkt treffen. Die Gitter, die wir betrachten sind die elf sogenannten uniformen Gitter. Diese beinhalten das Dreiecksgitter, das Vierecksgitter, das hexagonale und das trihexagonale Gitter. Als Symbol für das jeweilige Gitter werden die Polygone um einen Punkt herum benannt. Die Aufzählung wird mit dem Polygon mit der kleinsten Anzahl an Ecken begonnen [6]. Das Viereckgitter würde also das Symbol 4^4 bekommen, da sich an jedem Punkt vier Vierecke treffen. Beim trihexagonale Gitter treffen an jedem Punkt zwei Dreiecke und zwei Sechsecke abwechselnd aufeinander, deshalb wird es durch das Symbol 3.6.3.6 beschrieben.